在数据分析工作中，常常遇到一些指标系数，它的稳定性对于生产制造和质量控制来说至关重要。例如某地区快递条码扫描识别，平均识别率99.97%，这是挺不错的成绩。然而某天下大雨湿度大增，导致摄像头清晰度下降，识别率下降到96%。虽然整月平均值还在99.97%，但是那天的错误率从万分之三上升到4%，导致分错的包裹增加到133倍，这是非常致命的伤害。

问题背景

在各行各业的统计工作中，我们常常使用平均值来衡量一个指标。但是大家慢慢发现，平均值越来越“不公平”。常见的修正手段有：掐头去尾后平均、累计加权平均等等。这些小手段都只能适用于某些特定场景。于是，我们不妨思考，在数据统计这个领域，究竟有没有公认比较通用的方法。

以下回答来自于GPT4，预计未来一个月内，在星尘平台增加新指标。

解决方案

为了衡量同一个地区一段时间内某个指数（如XX率值）的稳定性，可以使用以下几个指标和算法：

标准差（Standard Deviation）:
标准差是衡量数据分散程度的常用指标，它是方差的平方根。计算同一个地区一段时间内XX率值的标准差可以帮助你了解该率值的波动程度。公式如下：
SD = √(Σ(xi - x̄)² / n)
其中，SD表示标准差，xi代表每一天的XX率值，x̄是这段时间内XX率值的平均值，n是观测值的数量。
变异系数（Coefficient of Variation，CV）:
变异系数是标准差与平均值的比率，通常用来比较不同量级或单位的数据的相对波动性。计算方法如下：
CV = (SD / x̄) × 100%
CV越大，表示XX率值的稳定性越差；CV越小，表示XX率值的稳定性越好。
时间序列分析:
如果你想更深入地分析XX率值的稳定性，可以使用时间序列分析的方法。例如，你可以构建一个自回归模型（AR模型）或移动平均模型（MA模型），或者结合两者的自回归移动平均模型（ARMA模型），来预测XX率值的未来走势，并分析其波动特征。
控制图（Control Charts）:
控制图是质量管理中使用的工具，用于监控过程是否处于控制状态。通过绘制XX率值的控制图，并设置控制限，可以直观地观察该率值是否存在异常波动。

在实际操作中，你可以根据数据的特性和分析的目的选择合适的指标和算法。通常，计算标准差和变异系数是比较简单直观的方法，适合初步评估稳定性。而时间序列分析和控制图则适用于更复杂的数据分析和长期监控。

实现代码：

// 平均值
public static double CalculateMean(List<double> values)
{
    double sum = values.Sum();
    return sum / values.Count;
}

// 标准差
public static double CalculateStandardDeviation(List<double> values)
{
    double mean = CalculateMean(values);
    double sumOfSquaresOfDifferences = values.Sum(val => (val - mean) * (val - mean));
    double standardDeviation = Math.Sqrt(sumOfSquaresOfDifferences / values.Count);
    return standardDeviation;
}

// 变异系数
public static double CalculateCoefficientOfVariation(List<double> values)
{
    double standardDeviation = CalculateStandardDeviation(values);
    double mean = CalculateMean(values);
    return (standardDeviation / mean) * 100;
}

// 时间序列分析，移动平均数
public static List<double> CalculateMovingAverage(List<double> values, int period)
{
    List<double> movingAverages = new List<double>();
    for (int i = 0; i <= values.Count - period; i++)
    {
        double sum = 0;
        for (int j = 0; j < period; j++)
        {
            sum += values[i + j];
        }
        movingAverages.Add(sum / period);
    }
    return movingAverages;
}

请注意，这里的时间序列分析仅仅是一个简单的移动平均计算，真正的时间序列分析可能涉及更复杂的数学模型，比如ARIMA模型，通常需要使用专门的统计软件或库（如R语言或Python的statsmodels库）来实现。

总结

在一个六西格玛理论中，学到一种简化版的控制图方法，可以衡量偏差是否过大导致异常。

控制图上限或下限，取3倍标准差。单独看上限，即：控制上限=平均值+标准差*3。全部除以平均值，得到变异系数表示，即：上限比率=控制上限/平均值=平均值/平均值+标准差*3/平均值=1+变异系数*3=1+CV*3。

因此，这里可以简单的认为，3倍变异系数，就是控制图上下限的边界比率。在实际操作中，需要根据情况来选择倍率。

这里3倍标准差的由来，跟概率密度函数有关。标准正态分布取3个标准差时，可以覆盖99.73%的范围。如果取4个标准差，可以覆盖99.99%的范围。

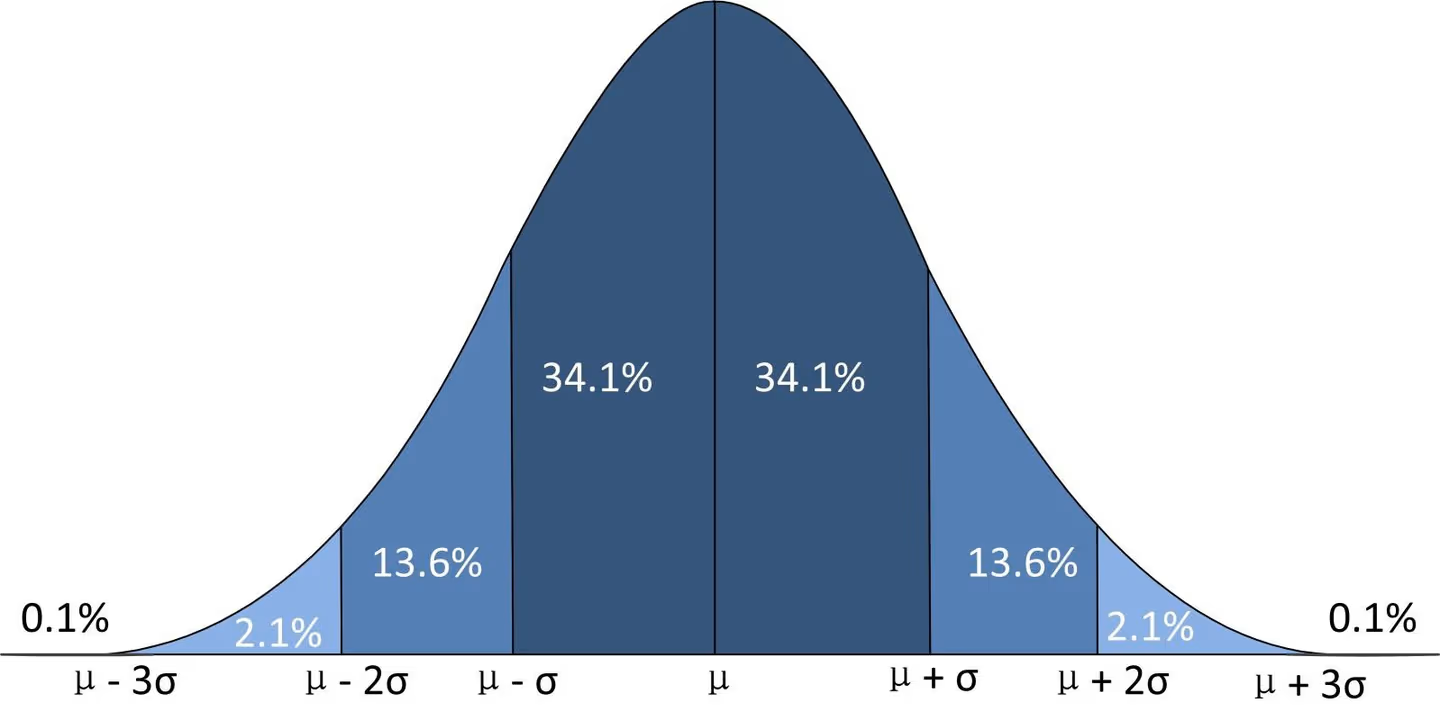
密度函数关于平均值对称

平均值与它的众数（statistical mode）以及中位数（median）同一数值。

函数曲线下68.268949%的面积在平均数左右的一个标准差范围内。

95.449974%的面积在平均数左右两个标准差的范围内。

99.730020%的面积在平均数左右三个标准差的范围内。

99.993666%的面积在平均数左右四个标准差的范围内。

综上所述，变异系数CV是一个很好的衡量数据稳定性的指标！

在数据分析中如何衡量指标稳定性

问题背景

解决方案

总结